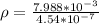Answer:
a
The mass of gold is
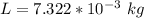
b
The volumes of gold and copper is
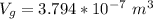 ,
,
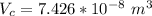
c
The density of the British sovereign coin

Step-by-step explanation:
From the question we are told that
The total mass of the gold is
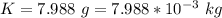
The karat of the British gold sovereign is
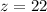
Let the mass of gold in the alloy be L
Now we are told that
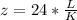
substituting value
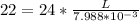
So
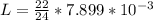
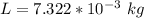
The volume of the gold coin is mathematically represented as
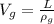
Where
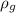 is the density of the gold which a constant with value
is the density of the gold which a constant with value
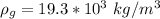
So
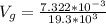
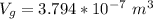
The mass of copper is mathematically evaluated as
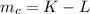
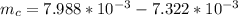
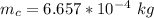
Volume of the copper is
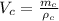
Where
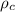 is the density of the copper which a constant with value
is the density of the copper which a constant with value

So
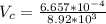
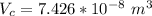
The total volume of the British gold sovereign coin is \

substituting values
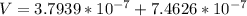
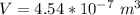
The density of the British gold sovereign coin is
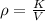
substituting values