Question

Consider a triangle ABC like the one below. Suppose that C equals 97° a equals 40 and b equals 17 sold the triangle carry your intermediate computations and to at least four decimal places around your house or to the nearest 10th if there are more than one solution use the button labeled or

Answer 1

c = 45.33, C =97°, a = 40, A = 61.15° , B = 21.85°, b = 17

Explanation:

Given that:

C = 97°, a = 40 and b = 17.

We have angle C, we need to find the side the side c opposite to the angle C. we have side a, we need to find the angle A opposite to side a. we have side b, we need to find the angle B opposite to side b.

Using cosine rule:

c² = a² + b² - 2ab × cos(C)

c² = 40² + 17² - 2(40)(17)cos(97)

c² = 2054.74

c = 45.33

Also using sine rule:

`(a)/(sin(A)) =(c)/(sin(C)) \\(40)/(sin(A))=(45.33)/(sin(97)) \\sin(A)=(sin(97))40)/(45.33)=0.876\\A=sin^(-1)(0.876)=61.15^0`

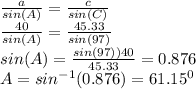
Also:

`(b)/(sin(B)) =(c)/(sin(C)) \\(17)/(sin(B))=(45.33)/(sin(97)) \\sin(B)=(sin(97))17)/(45.33)=0.3722\\B=sin^(-1)(0.3722)=21.85^0`

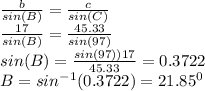
c = 45.33, C =97°, a = 40, A = 61.15° , B = 21.85°, b = 17