Answer:
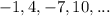 neither
neither
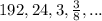 geometric progression
geometric progression
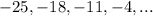 arithmetic progression
arithmetic progression
Explanation:
Given:
sequences:
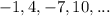
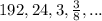
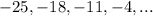
To find: which of the given sequence forms arithmetic progression, geometric progression or neither of them
Solution:
A sequence forms an arithmetic progression if difference between terms remain same.
A sequence forms a geometric progression if ratio of the consecutive terms is same.
For
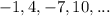 :
:
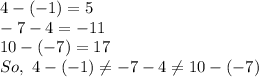
Hence,the given sequence does not form an arithmetic progression.
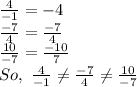
Hence,the given sequence does not form a geometric progression.
So,
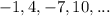 is neither an arithmetic progression nor a geometric progression.
is neither an arithmetic progression nor a geometric progression.
For
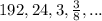 :
:
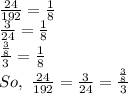
As ratio of the consecutive terms is same, the sequence forms a geometric progression.
For
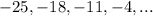 :
:

As the difference between the consecutive terms is the same, the sequence forms an arithmetic progression.