Question

Solve the system by using a matrix equation

7x-4y=4

10x-6y=2

Answer 1

The solution to the system of equation is x = 8, y = 13

Explanation:

The system of equation using matrix equation can be solved using crammers rule. Given the equation;

7x-4y=4

10x-6y=2

The equation will be rewritten in the format AX = B

matrix A will be 2*2 matrix

X will be a column matrix containing the variables

B will be a column matrix

`\left[\begin{array}{cc}7&-4\\10&-6\\\end{array}\right] \left[\begin{array}{c}x&y\\\\\end{array}\right] = \right] \left[\begin{array}{c}4&2\\\\\end{array}\right]`

first we will find the determinant of the matrix A

`|A|=7(-6)-(10)(-4)\\|A|= -42+40\\|A|= -2`

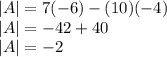
To get the value of x, we will substitute the column matrix at the right hand side to replace the first column pf matrix A, then we look for the determinant and divide the determinant by the determinant of matrix A itself.

`|X|=\left[\begin{array}{cc}4&-4\\2&-6\\\end{array}\right]\\|X|= -24+8\\|X|=-16`

x = |X|/|A|

x = -16/-2

x = 8

Similarly for y, we will substitute the column matrix at the right hand side to replace the second column of matrix A, then we look for the determinant and divide the determinant by the determinant of matrix A itself.

`|Y|=\left[\begin{array}{cc}7&4\\10&2\\\end{array}\right]\\|Y|= 14-40\\|Y|=-26`

y = |Y|/|A|

y = -26/-2

y = 13

The solution to the system of equation is x = 8, y = 13