Question

wyatt is designing a hollow cylindrical metal can with volume 1000 cm3.the materialused to make the circular top and bottom of the can costs twice as much as the material used tomake the side of the can. what dimensions should wyatt choose in order to minimize the cost ofthe can?show all your work, round off the numerical part of your final answer to four (4) decimal places,and express your final answer in the form of a complete sentence, using the correct units.

Answer 1

Step-by-step explanation:

Let r be the radius of circular top and h be the height of the cylinder

Given

π r² h = 1000

Let cost of making side of can be p per unit area , the cost of making top and bottom will be 2p per unit area.

total cost

C = 2 x π r² x 2p + 2πrh x p

= 2(1000 / h) x 2p + 2π x (1000 / π) x
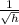`(1)/(√(h) )` x h x p

= 2(1000 / h) x 2p + 2π x (1000 / π) x √h x p

differenciating

dC / dh = 2(- 1000 / h²) x 2p + 2π x (1000 / π) x
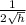`(1)/(2√(h) )` x p = 0 for minimum cost

- 4 / h² + 1 / √h = 0

h³ = 16

h = 2.519 cm .

π r² h = 1000

π r² x 2.519 = 1000

r = 11.24 cm

The cylinder will have height of 2.519 cm and radius of 11.24 cm.