Question

An online retailer has determined that the average time for credit card transactions to be electronically approved is 1.8 seconds. (Round your answers to three decimal places.) (a) Use an exponential density function to find the probability that a customer waits less than a second for credit card approval. (b) Find the probability that a customer waits more than 3 seconds. (c) What is the minimum approval time for the slowest 5% of transactions

Answer 1

a) 0.426 = 42.6% probability that a customer waits less than a second for credit card approval.

b) 0.189 = 18.9% probability that a customer waits more than 3 seconds.

c) The minimum approval time for the slowest 5% of transactions is 5.39 seconds.

Explanation:

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

`f(x) = \mu e^(-\mu x)`

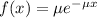
In which
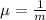`\mu = (1)/(m)` is the decay parameter.

The probability that x is lower or equal to a is given by:

`P(X \leq x) = \int\limits^a_0 {f(x)} \, dx`

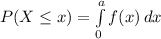
Which has the following solution:

`P(X \leq x) = 1 - e^(-\mu x)`

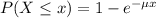
The probability of finding a value higher than x is:

`P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^(-\mu x)) = e^(-\mu x)`

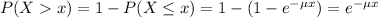
An online retailer has determined that the average time for credit card transactions to be electronically approved is 1.8 seconds.

This means that
`m = 1.8, \mu = (1)/(1.8) = 0.5555`

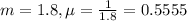
(a) Use an exponential density function to find the probability that a customer waits less than a second for credit card approval.

This is
`P(X \leq 1)`.

`P(X \leq 1) = 1 - e^(-0.5555*1) = 0.426`

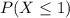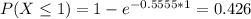
0.426 = 42.6% probability that a customer waits less than a second for credit card approval.

(b) Find the probability that a customer waits more than 3 seconds.

This is P(X > 3).

`P(X > x) = 1 - P(X \leq 3) = 1 - (1 - e^(-0.5555*3)) = 0.189`

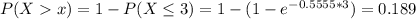
0.189 = 18.9% probability that a customer waits more than 3 seconds.

(c) What is the minimum approval time for the slowest 5% of transactions

This is x for which
`P(X \leq x) = 0.95`

So

`P(X \leq x) = 1 - e^(-\mu x)`

`0.95 = 1 - e^(-0.5555x)`

`e^(-0.5555x) = 0.05`

`\ln{e^(-0.5555x)} = ln(0.05)`

`-0.5555x = ln(0.05)`

`x = -(ln(0.05))/(0.5555)`

`x = 5.39`

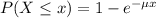
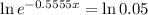
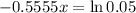
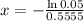
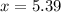
The minimum approval time for the slowest 5% of transactions is 5.39 seconds.