Question

If a polynomial function f(x) has roots 0, 3, and 2+ V5, what must also be a root of f(x)?

-2-sqrt15
2-sqrt15
15-sqrt 2
15+sqrt 2

Answer 1

B)

Explanation:

Answer 2

Option B.

Explanation:

Note: Given roots are not in proper format.

Consider the polynomial function f(x) has roots 0, 3, and
`2+√(15)`.

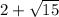According to irrational root theorem if
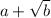`a+√(b)` is root of a polynomial P(x), then
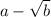`a-√(b)` is also a root of polynomial P(x).

Since
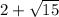`2+√(15)` is an irrational root of the function f(x). By irrational root theorem
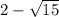`2-√(15)` is also a root of function f(x).

Therefore, the correct option is B.