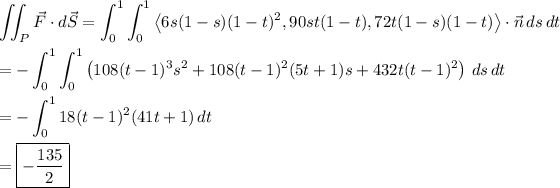Question

Compute the flux of the vector field F = xy, 5yz, 6zx through the portion of the plane 3x + 2y + z = 6 in the first octant with the downward orientation.

Answer 1

The plane has intercepts

y = z = 0 ⇒ 3x = 6 ⇒ x = 2

x = z = 0 ⇒ 2y = 6 ⇒ y = 3

x = y = 0 ⇒ z = 6

and thus passes through the points (2, 0, 0), (0, 3, 0), and (0, 0, 6).

Parameterize the portion of the plane (call it P) by the vector function,

`\vec r(s,t) = \left\langle 2(1-s)(1-t), 3s(1-t), 6t \right\rangle`

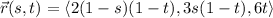
where 0 ≤ s ≤ 1 and 0 ≤ t ≤ 1.

Compute the normal vector to P :

`\vec n = (\partial \vec r)/(\partial t) * (\partial \vec r)/(\partial s) = -\left\langle 18-18t, 12-12t, 6-6t \right\rangle`

Then the flux of F through P is given by the surface integral,

`\displaystyle \iint_P \vec F \cdot d\vec S = \int_0^1 \int_0^1 \left\langle 6s(1-s)(1-t)^2, 90st(1-t), 72t(1-s)(1-t) \right\rangle \cdot \vec n \, ds \, dt \\\\ = - \int_0^1 \int_0^1 \left(108(t-1)^3 s^2 + 108(t-1)^2(5t+1) s + 432t(t-1)^2\right) \, ds \, dt \\\\ = - \int_0^1 18(t-1)^2(41t+1) \, dt \\\\ = \boxed{-\frac{135}2}`