Question

Suppose that output (Y ) in an economy is given by the following aggregate production function: Yt = Kt + Nt where Kt is capital and Nt is the population. Furthermore, assume that capital depreciates at rate δ and that savings is a constant proportion s of income. You may assume that δ > s. 1. Suppose that the population remains constant. Solve for the steady-state level of capital per worker. 2. Now suppose that the population grows at rate n. Solve for the steady-state level of capital per worker. 3. Based on your answer to part 2) above, solve for the steady-state growth rates (in terms of n) of the following: (a) capital per worker (b) output per worker (c) capital (d) output

Answer 1

Check the explanation

Step-by-step explanation:

Yt = Kt + Nt

Taking output per worker, we divide by Nt

Yt/Nt = Kt/Nt + 1

yt = kt + 1

where yt is output per worker and kt is capital per worker.

a) With population being constant, savings rate s and depreciation rate δ.

ΔKt = It - δKt

dividing by Nt, we get

ΔKt/Nt = It/Nt - δKt/Nt ..... [1]

for kt = Kt/Nt, taking derivative

d(kt)/dt = d(Kt/Nt)/dt ... since Nt is a constant, we have

d(kt)/dt = d(Kt/Nt)/dt = (dKt/dt)/Nt = ΔKt/Nt = It/Nt - δKt/Nt = it - δkt

thus, Capital accumulation Δkt = i – δkt

In steady state, Δkt = 0

That is I – δkt = 0

S = I means that I = s.yt

Thus, s.yt – δkt = 0

Then kt* = s/δ(yt) = s(kt+1)/(δ )

kt*= skt/(δ) + s/(δ)

kt* - skt*/(δ) = s/(δ)

kt*(1- s/(δ) = s/(δ)

kt*((δ - s)/(δ) = s/(δ)

kt*(δ-s)) = s

kt* = s/(δ -s)

capital per worker is given by kt*

b) with population growth rate of n,

d(kt)/dt = d(Kt/Nt)/dt =

=
`((dKt)/(dt)Nt - (dNt)/(dt)Kt)/(N^(2)t)`

=
`(dKt/dt)/(Nt) - (dNt/dt)/(Nt).(Kt)/(Nt)`

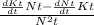
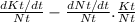
= ΔKt/Nt - n.kt

because (dNt/dt)/Nt = growth rate of population = n and Kt/Nt = kt (capital per worker)

so, d(kt)/dt = ΔKt/Nt - n.kt

Δkt = ΔKt/Nt - n.kt = It/Nt - δKt/Nt - n.kt ......(from [1])

Δkt = it - δkt - n.kt

at steady state Δkt = it - δkt - n.kt = 0

s.yt - (δ + n)kt = 0........... since it = s.yt

kt* = s.yt/(δ + n) =s(kt+1)/(δ + n)

kt*= skt/(δ + n) + s/(δ + n)

kt* - skt*/(δ + n) = s/(δ + n)

kt*(1- s/(δ + n)) = s/(δ + n)

kt*((δ + n - s)/(δ + n)) = s/(δ + n)

kt*(δ + n -s)) = s

kt* = s/(δ + n -s)

.... is the steady state level of capital per worker with population growth rate of n.

3. a) capital per worker. in steady state Δkt = 0 therefore, growth rate of kt is zero

b) output per worker, yt = kt + 1

g(yt) = g(kt) = 0

since capital per worker is not growing, output per worker also does not grow.

c)capital.

kt* = s/(δ + n -s)

Kt*/Nt = s/(δ + n -s)

Kt* = sNt/(δ + n -s)

taking derivative with respect to t.

d(Kt*)/dt = s/(δ + n -s). dNt/dt

(dNt/dt)/N =n (population growth rate)

so dNt/dt = n.Nt

d(Kt*)/dt = s/(δ + n -s).n.Nt

dividing by Kt*

(d(Kt*)/dt)/Kt* = s/(δ + n -s).n.Nt/Kt* = sn/(δ + n -s). (Nt/Kt)

`(sn)/(\delta +n-s).(Nt)/(Kt)`

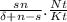
using K/N = k

`(s)/(\delta +n-s).(n)/(kt)`

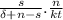
plugging the value of kt*

`(sn)/(\delta +n-s).((\delta + n -s))/(s)`

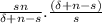
n

thus, Capital K grows at rate n

d) Yt = Kt + Nt

dYt/dt = dKt/dt + dNt/dt = s/(δ + n -s).n.Nt + n.Nt

using d(Kt*)/dt = s/(δ + n -s).n.Nt from previous part and that (dNt/dt)/N =n

dYt/dt = n.Nt(s/(δ + n -s) + 1) = n.Nt(s+ δ + n -s)/(δ + n -s) = n.Nt((δ + n)/(δ + n -s)

dYt/dt = n.Nt((δ + n)/(δ + n -s)

dividing by Yt

g(Yt) = n.(δ + n)/(δ + n -s).Nt/Yt

since Yt/Nt = yt

g(Yt) = n.(δ + n)/(δ + n -s) (1/yt)

at kt* = s/(δ + n -s), yt* = kt* + 1

so yt* = s/(δ + n -s) + 1 = (s + δ + n -s)/(δ + n -s) = (δ + n)/(δ + n -s)

thus, g(Yt) = n.(δ + n)/(δ + n -s) (1/yt) = n.(δ + n)/(δ + n -s) ((δ + n -s)/(δ + n)) = n

therefore, in steady state Yt grows at rate n.