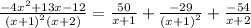Question

(HURRY! I'M BEING TIMED)Write the partial fraction decomposition of the rational expression.

(-4x^2+13x-12)/((x+2)(x+1)^2)

Answer 1

The partial fraction decomposition is
`(- 4 x^(2) + 13 x - 12)/(\left(x + 1\right)^(2) \left(x + 2\right))=(50)/(x + 1)+(-29)/(\left(x + 1\right)^(2))+(-54)/(x + 2)`.

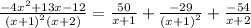Explanation:

Partial-fraction decomposition is the process of starting with the simplified answer and taking it back apart, of "decomposing" the final expression into its initial polynomial fractions.

To find the partial fraction decomposition of
`(- 4 x^(2) + 13 x - 12)/(\left(x + 1\right)^(2) \left(x + 2\right))`:

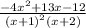First, the form of the partial fraction decomposition is

`(- 4 x^(2) + 13 x - 12)/(\left(x + 1\right)^(2) \left(x + 2\right))=(A)/(x + 1)+(B)/(\left(x + 1\right)^(2))+(C)/(x + 2)`

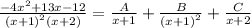
Write the right-hand side as a single fraction:

`(- 4 x^(2) + 13 x - 12)/(\left(x + 1\right)^(2) \left(x + 2\right))=(\left(x + 1\right)^(2) C + \left(x + 1\right) \left(x + 2\right) A + \left(x + 2\right) B)/(\left(x + 1\right)^(2) \left(x + 2\right))`

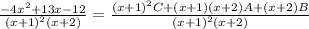
The denominators are equal, so we require the equality of the numerators:

`- 4 x^(2) + 13 x - 12=\left(x + 1\right)^(2) C + \left(x + 1\right) \left(x + 2\right) A + \left(x + 2\right) B`

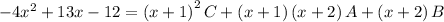
Expand the right-hand side:

`- 4 x^(2) + 13 x - 12=x^(2) A + x^(2) C + 3 x A + x B + 2 x C + 2 A + 2 B + C`

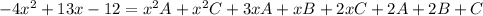
The coefficients near the like terms should be equal, so the following system is obtained:

`\begin{cases} A + C = -4\\3 A + B + 2 C = 13\\2 A + 2 B + C = -12 \end{cases}`

Solving this system, we get that
`A=50, B=-29, C=-54`.

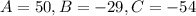Therefore,

`(- 4 x^(2) + 13 x - 12)/(\left(x + 1\right)^(2) \left(x + 2\right))=(50)/(x + 1)+(-29)/(\left(x + 1\right)^(2))+(-54)/(x + 2)`