Question

An airline is planning its staffing needs for the next year. If a new route is​ approved, it will hire 858 new employees. If a new route is not​ granted, it will hire only 157 new employees. If the probability that a new route will be granted is 0.34 ​, what is the expected number of new employees to be hired by the​ airline?

Answer 1

`E(X) = \sum_(i=1)^n X_i P(X_i)`

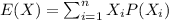
And from the problem we know the following:

`P(X_1) = 0.34 , X_1 =858` represent the condition if the route is approved

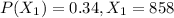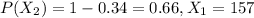`P(X_2) = 1-0.34=0.66 , X_1 =157` represent the condition if the route is NOT approved

Then replacing in the formula for the expected value we got:

`E(X) = 858*0.34 + 157*0.66 = 395.34`

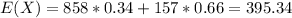
So then the expected number of new employees to be hired by the​ airline based on the conditions given is between 395 and 396.

Explanation:

For this cae we can define the random variable X who represent the number of new employees to be hired by the​ airline and we can find the expected value with the following general formula:

`E(X) = \sum_(i=1)^n X_i P(X_i)`

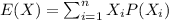
And from the problem we know the following:

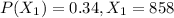`P(X_1) = 0.34 , X_1 =858` represent the condition if the route is approved

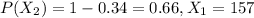`P(X_2) = 1-0.34=0.66 , X_1 =157` represent the condition if the route is NOT approved

Then replacing in the formula for the expected value we got:

`E(X) = 858*0.34 + 157*0.66 = 395.34`

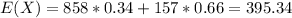
So then the expected number of new employees to be hired by the​ airline based on the conditions given is between 395 and 396.