Question

Keegan is printing and selling his original design on t-shirts. He has concluded that for x shirts, in thousands sold his total profits will be p(x) = dollars, in thousands will be earned. How may t-shirts (rounded to the nearest whole number) should he print in order to make maximum profits? What will his profits rounded to the nearest whole dollar be if he prints that number of shirts?

Answer 1

t-shirts: 2790

profit: $12209

Explanation:

Given the function:

p(x) = -x³ + 4x² + x

we want to maximize it.

The following criteria must be satisfied at the maximum:

dp/dx = 0

d²p/dx² < 0

dp/dx = -3x² + 8x + 1 = 0

Using quadratic formula:

`x = (-b \pm √(b^2 -4(a)(c)))/(2(a))`

`x = (-8 \pm √(8^2 -4(-3)(1)))/(2(-3))`

`x = (-8 \pm 8.72)/(-6)`

`x_1 = (-8 + 8.72)/(-6)`

`x_1 = -0.12`

`x_2 = (-8 - 8.72)/(-6)`

`x_2 = 2.79`

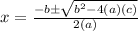
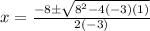
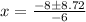
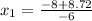
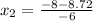
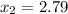
d²p/dx² = -6x + 8

d²p/dx² at x = -0.12: -6(-0.12) + 8 = 8.72 > 0

d²p/dx² at x = 2.79: -6(2.79) + 8 = -8.74 < 0

Then, he should prints 2.79 thousands, that is, 2790 t-shirts to make maximum profits.

Replacing into profit equation:

p(x) = -(2.79)³ + 4(2.79)² + 2.79 = 12.209

that is, $12209