Question

Find x in this 45°-45°-90° triangle.

Answer 1

The length of
`\( x \)` in the triangle is 9 units. Therefore, the correct answer from the provided options is 9.

In a 45°-45°-90° triangle, the sides have a specific ratio: the length of the hypotenuse is
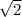`\( √(2) \)` times the length of each of the other two sides, which are of equal length. This type of triangle is sometimes referred to as an isosceles right triangle.

Given that the hypotenuse is
`\( 9√(2) \)` and we need to find the length of one of the legs (x), we can use the relationship:

`\[ \text{Hypotenuse} = x√(2) \]`

`\[ 9√(2) = x√(2) \]`

Solving for x:

`\[ x = (9√(2))/(√(2)) \]`

`\[ x = 9 \]`

The length of
`\( x \)` in the triangle is 9 units. Therefore, the correct answer from the provided options is 9.

Answer 2

Answer: I think it should be 4.5

Explanation: