Question

(cot^2x - 1)/(csc^2x) = cos2x​

Answer 1

Explanation:

The idea here is to get the left side simplified down so it is the same as the right side. Consequently, there are 3 identities for cos(2x):

`cos(2x)=cos^2x-sin^2x`,

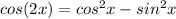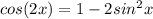`cos(2x)=1-2sin^2x`, and

`cos(2x)=2cos^2x-1`

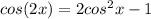
We begin by rewriting the left side in terms of sin and cos, since all the identities deal with sines and cosines and no cotangents or cosecants. Rewriting gives you:

`((cos^2x)/(sin^2x) -(sin^2x)/(sin^2x) )/((1)/(sin^2x) )`

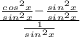
Notice I also wrote the 1 in terms of sin^2(x).

Now we will put the numerator of the bigger fraction over the common denominator:

`((cos^2x-sin^2x)/(sin^2x) )/((1)/(sin^2x) )`

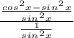
The rule is bring up the lower fraction and flip it to multiply, so that will give us:

`(cos^2x-sin^2x)/(sin^2x) *(sin^2x)/(1)`

And canceling out the sin^2 x leaves us with just

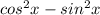`cos^2x-sin^2x` which is one of our identities.