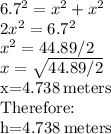Answer:
x=4.738 meters
h=4.738 meters
Explanation:
a = length of the ladder.
h = height of the ladder’s top at time t, and
x = distance from the wall to the ladder’s bottom.
From Pythagoras Theorem
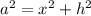
If a=6.7 meters, then:
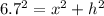
The top is sliding down the wall(decreasing) at a rate of 0.2m/s, therefore:

If the top and bottom of the ladder move at the same speed, then:
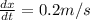
Taking derivative of
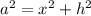
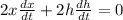

From
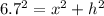
Since x=h