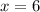Question

Part of the roof of a factory is devoted to mechanical support and part to green space. The area G that is designated as green space can be modeled by the polynomial 2x2 - 7x and the area M that is devoted to mechanical support can be modeled by the polynomial x2 - 9x + 24. Given that the area R of the roof is 36 square yards, write and solve a quadratic equation to find the total area of the green space. **Use the positive value for your solution.

(Hint: R = G + M)

Answer 1

`36 = 2x^2 -7x +x^2 -9x +24`

`12= 3x^2 -16 x`

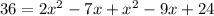
And we can rewrite this expression like this:

`3x^2 -16 x -12 =0`

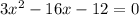
And we can use the quadratic formual to solve this problem:

`X =(-b \pm √(b^2 -4ac))/(2a)`

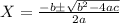
With a = 3, b = -16 , c =-12. Replacing we got:

`x = (16 \pm √((-16)^2 -4*(3)*(-12)))/(2*3)`

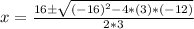
And the solutions for this case are:

`x_1 = 6, x_2 =-(2)/(3)`

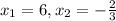
And then since we need to select the positive solution the final answer would be:

`x = 6`

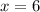
Explanation:

For this case we have the following equations for the total area of the green space:

`G = 2x^2 -7x`

`M = x^2 -9x +24`

And the total area is given by 36 yd^2. And we know that:

`R = 36 yd^2 = G+M`

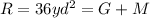
Replacing the info given we got:

`36 = 2x^2 -7x +x^2 -9x +24`

`12= 3x^2 -16 x`

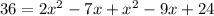
And we can rewrite this expression like this:

`3x^2 -16 x -12 =0`

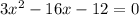
And we can use the quadratic formual to solve this problem:

`X =(-b \pm √(b^2 -4ac))/(2a)`

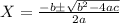
With a = 3, b = -16 , c =-12. Replacing we got:

`x = (16 \pm √((-16)^2 -4*(3)*(-12)))/(2*3)`

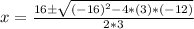
And the solutions for this case are:

`x_1 = 6, x_2 =-(2)/(3)`

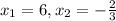
And then since we need to select the positive solution the final answer would be:

`x = 6`