Question

Two similar cones have heights of 9 cm and 4 cm. Find the ratio of their volumes

Answer 1

The ratio of their volumes is:
`(729)/(64)`

Explanation:

If the cones are similar, then the ratio of their heights should equal the ratio of their radiuses. If we call R the radius of the larger cone (the one of height 9 cm) and r the radius of the smaller cone (the one of height 4 cm), then the following proportion should be verified:

`(R)/(r) =(9)/(4) \\R=(9\,r)/(4)`

where we have solved for "R" in terms of "r".

Now we input this information in the formula for the volume (V) of the largest cone, and for the volume (v) of the smaller cone, recalling that the volume of a cone is the product of the area of the cone's circular base (
`\pi *\,radius^2`).

`v=(\pi\,r^2\,4\,)/(3) =\pi r^2\,(4)/(3) \\V=(\pi\,R^2\,9)/(3)=(\pi\,((9\,r)/(4) )^2\,9)/(3)=(\pi\,r^2\,729)/(16*3)=\pi r^2\,(243)/(16)`

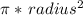So now the ratio of their volumes (V/v) can be obtained:

`(V)/(v) =((243)/(16))/((4)/(3)) =(729)/(64)`