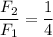Question

A satellite and the International Space Station have the same mass and are going around Earth in concentric orbits. The distance of the satellite from Earth\'s center is twice that of the International Space Station\'s distance. What is the ratio of the centripetal force acting on the satellite compared to that acting on the International Space Station

Answer 1

`(F_2)/(F_1)=(1)/(4)`

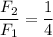
Step-by-step explanation:

G = Gravitational constant

r = Distance between Earth and object

M = Mass of Earth

m = Mass of object

Centripetal force on the space station

`F_1=(GMm)/(r^2)`

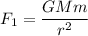
Centripetal force on the satellite

`F_2=(GMm)/((2r)^2)\\\Rightarrow F_2=(GMm)/(4r^2)`

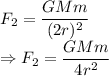
From the question the required ratio is

`(F_2)/(F_1)=((GMm)/(4r^2))/((GMm)/(r^2))\\\Rightarrow (F_2)/(F_1)=(1)/(4)`

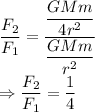
The ratio is
`(F_2)/(F_1)=(1)/(4)`