Question

Using the traditional formula, a 95% CI for p1 − p2 is to be constructed based on equal sample sizes from the two populations. For what value n (= m) will the resulting interval have width at most 0.4 irrespective of the results of the sampling? (Round your answer up to the nearest whole number.)

Answer 1

The minimum sample size required is 49.

Explanation:

The (1 - α)% confidence interval for the difference between two proportions is:

`CI=(\hat p_(1)-\hat p_(2))\pm z_(\alpha/2)\ \sqrt{(\hat p_(1)(1-\hat p_(1))+\hat p_(2)(1-\hat p_(2)))/(n)}`

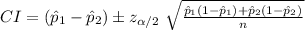
*The sample size is considered equal in this case.

The width of the interval is at most 0.40.

Then the margin of error of the interval will be:

MOE = Width ÷ 2 = 0.20

The formula of the margin of error is:

`MOE= z_(\alpha/2)\ \sqrt{(\hat p_(1)(1-\hat p_(1))+\hat p_(2)(1-\hat p_(2)))/(n)}`

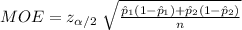
Assume that the two sample proportion values are 0.50.

The critical value of z for 95% confidence level is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

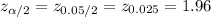
Compute the sample size required as follows:

`MOE= z_(\alpha/2)\ \sqrt{(\hat p_(1)(1-\hat p_(1))+\hat p_(2)(1-\hat p_(2)))/(n)}`

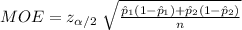
`n=[\frac{z_(\alpha/2)* \sqrt{\hat p_(1)(1-\hat p_(1))+\hat p_(2)(1-\hat p_(2))}}{MOE}]^(2)`

`=[(1.96* √(0.50(1-0.50)+0.50(1-0.50)))/(0.20)]^(2)\\\\=48.02\\\\\approx 49`

Thus, the minimum sample size required is 49.