Question

Find all the critical points of h(x) = x^3 − 3x^4 and categorize them as local

maximums, local minimums, or neither, using the first derivative test.

Answer 1

0 is an inflection point

1/4 is a local maximum.

Explanation:

To begin with you find the first derivative of the function and get that

`h'(x) = 3x^2 - 12x^3`

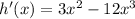
to find the critical points you equal the first derivative to 0 and get that

`3x^2 - 12x^3 = 0, x = 0,1/4`

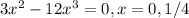
To find if they are maximums or local minimums you use the second derivative.

`h''(x) = 6x-36x^2`

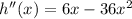
since
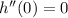`h''(0) = 0` is neither an inflection point, and since
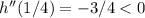`h''(1/4) = -3/4 <0` then 1/4 is a maximum.