Question

A 50 mm diameter steel shaft and a 100 mm long steel cylindrical bushing with an outer diameter of 70 mm have been incorrectly shrink fit together and have to be separated. What axial force, Pa, is needed for this if the diametral interference is 0.005 mm and the coefficient of friction is 0.2? E (steel) = 207 x 103 MPa (N/mm2)

Answer 1

The axial force is
`P = 15.93 k N`

Step-by-step explanation:

From the question we are told that

The diameter of the shaft steel is
`d = 50mm`

The length of the cylindrical bushing
`L =100mm`

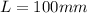
The outer diameter of the cylindrical bushing is
`D = 70 \ mm`

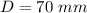
The diametral interference is
`\delta _d = 0.005 mm`

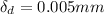
The coefficient of friction is
`\mu = 0.2`

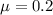
The Young modulus of steel is
`207 *10^(3) MPa (N/mm^2)`

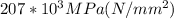
The diametral interference is mathematically represented as

`\delta_d = (2 *d * P_B * D^2)/(E (D^2 -d^2))`

Where
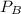`P_B` is the pressure (stress) on the two object held together

So making
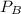`P_B` the subject

`P_B = (\delta _d E (D^2 - d^2))/(2 * d* D^2)`

Substituting values

`P_B = ((0.005) (207 *10^(3) ) * (70^2 - 50^2)))/(2 * (50) (70) ^2 )`

`P_B = 5.069 MPa`

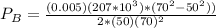
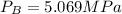
Now he axial force required is

`P = \mu * P_B * A`

Where A is the area which is mathematically evaluated as

`\pi d l`

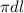
So
`P = \mu P_B \pi d l`

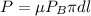
Substituting values

`P = 0.2 * 5.069 * 3.142 * 50 * 100`

`P = 15.93 k N`