The height of a right circular cylinder is 1.5 times the radius of the base. What is the ratio of the total surface area to the lateral (curved) surface area of the cylinder?

Question

asked Mar 14, 2021 54.5k views

1 Answer

XoXo · Answer 1 · 2021-03-18T12:43:23+0000

Let r represent the radius of cylinder.

We have been given that the height of a right circular cylinder is 1.5 times the radius of the base. So the height of the cylinder would be
1.5r .

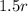We will use lateral surface area of pyramid to solve our given problem.

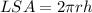$LSA=2\pi r h$ , where,

LSA = Lateral surface area of pyramid,

r = Radius,

h = height.

Upon substituting our given values in above formula, we will get:

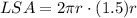
$LSA=2\pi r\cdot (1.5)r$

Now we will find the total surface area of cylinder.

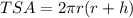
$TSA=2\pi r(r+h)$

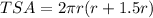
$TSA=2\pi r(r+1.5r)$

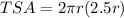
$TSA=2\pi r(2.5r)$

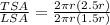
$(TSA)/(LSA)=(2\pi r(2.5r))/(2\pi r(1.5r))$

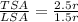
(TSA)/(LSA)=(2.5r)/(1.5r)

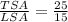
(TSA)/(LSA)=(25)/(15)

(TSA)/(LSA)=(5)/(3)

Therefore, the ratio of total surface area to lateral surface area is
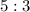5:3 .