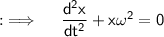Question

The position x of a particle moving along x axis varies with time t as x = Asin(wt) , where A and w are constants . The acceleration of the particle varies with its position as


`\small \red{ \rm Nonsense = Report} \checkmark`
​

Answer 1

Given that the position x of a particle along X-axis varies with time t by the equation:

`{:\implies \quad \sf x=A\sin (\omega t)}`

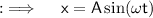
As it defines the position, so x is just displacement here, and we need to find the acceleration first for telling with what if varies, so by definition, the second differential coefficient of displacement is acceleration, so differentiating both sides w.r.t.x of the above equation in accordance with chain rule we have:

`{:\implies \quad \sf (dx)/(dt)=A\cos (\omega t)\cdot \omega \cdot (dt)/(dt)}`

`{:\implies \quad \sf (dx)/(dt)=A\omega \cos (\omega t)}`

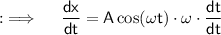
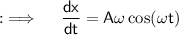
Differentiating both sides w.r.t.x by chain rule again to get the 2nd order derivative

`{:\implies \quad \sf (d^(2)x)/(dt^(2))=-A\omega \sin (\omega t)\cdot \omega (dt)/(dt)}`

`{:\implies \quad \sf (d^(2)x)/(dt^(2))=-A\omega^(2)\sin (\omega t)}`

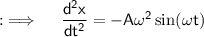
Re-write as :

`{:\implies \quad \sf (d^(2)x)/(dt^(2))=-\omega^(2)\{A\sin (\omega t)\}}`

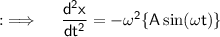
Can be further written as

`{:\implies \quad \sf (d^(2)x)/(dt^(2))=-x\omega^(2)}`

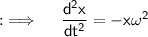
This is the Required answer

If they ask you the differential equation for the acceleration of a wave (as the given equation was general equation of a wave), you can simply write:

`{:\implies \quad \sf (d^(2)x)/(dt^(2))+x\omega^(2)=0}`

Answer 2

Let's see

`\\ \rm\Rrightarrow x=Asin(\omega t)\dots(1)`

Now we know the formula of acceleration

`\\ \rm\Rrightarrow \alpha=-A\omega^2sin(\omega t)`

`\\ \rm\Rrightarrow \alpha=-Asin(\omega t)* \omega^2`

• From eq(1)

`\\ \rm\Rrightarrow \alpha=-x\omega^2`

Or

`\\ \rm\Rrightarrow \alpha=-\omega^2x`