Answer:
(a)
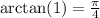
(b)

(c)
Therefore if you sum any three terms of it you get the desired accuracy.
(d)
If you sum 1999 terms you get the desired accuracy.
Explanation:
From the information given we know that
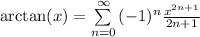
(a)
For that you need to find and angle
 such that
such that
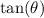 = 1, remember that
= 1, remember that
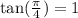 therefore
therefore
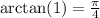
(b)
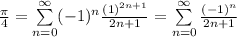
Then you just multiply by 4 and get that

(c)
Using the alternating series test, since the sequence
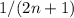 is decreasing and its limit tends to 0 when n tends to infinity the series is convergent.
is decreasing and its limit tends to 0 when n tends to infinity the series is convergent.
(d)
Using the estimation theorem of alternating series we know that if
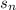 denotes the partial sum of the series then
denotes the partial sum of the series then
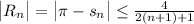
Therefore we are looking for an
 such that
such that
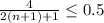
we just have to solve that inequality, when you solve that inequality you get that
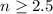
Therefore if you sum any three terms of it you get the desired accuracy.
(e) For this part you need to solve the following inequality
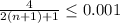
When you solve that inequality you get that
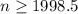
so, if you sum 1999 terms you get the desired accuracy.