Answer:
The correct option is (A).
Explanation:
The (1 - α)% confidence interval for difference in proportion formula is,

The given information is:
n₁ = n₂ = 200,
X₁ = 1062,
X₂ = 900.
Compute the sample proportion as follows:
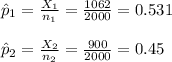
For the 95% confidence level, the z-value is,
z₀.₀₂₅ = 1.96
*Use a z-table.
Compute the 95% confidence interval for the difference in proportion as follows:

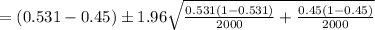
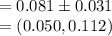
Thus, the 95% confidence interval for the difference in proportion of registered voters that support this candidate between the northern and southern halves of the state is (0.050, 0.112).
The correct option is (A).