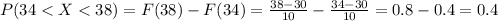Answer:
a)
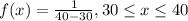
b)
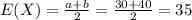
c)
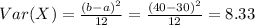
And the deviation would be:
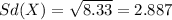
d)
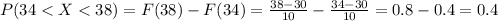
Explanation:
For this case we define the random variable X with this distribution:
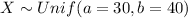
Part a
The density function since is an uniform distribution is given by:
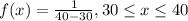
Part b
The expected value is given by:
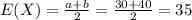
Part c
The variance is given by:
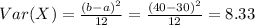
And the deviation would be:
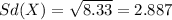
Part d
For this case we want this probability:
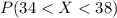
And we can use the cumulative distribution function given by:
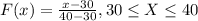
And using this we got: