Answer:
The counterclockwise circulation is
 and the outward flux is
and the outward flux is
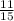
Explanation:
We are given the field
 . A picture of the region and the path we are considering is attached. Recalll the following theorems.
. A picture of the region and the path we are considering is attached. Recalll the following theorems.
Given a field of the form F(x,y)=(f(x,y),g(x,y) with f,g having continous partial derivates, C is a closed path counterclockwise oriented, R is the region enclosed by C and n is the normal vector pointing outwards of the path C. Then
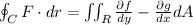 (this one calculates the counterclockwise circulation)
(this one calculates the counterclockwise circulation)
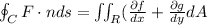 (This one calculates the outward flux)
(This one calculates the outward flux)
Then, recall that in our case f(x,y) = 7xy, g(x,y)=2y^2[/tex]. Then

 .
.
Note that we just need to describe our region R. The region R lies between the parabola y=x^2 and the line y=x. Thus, one way to describe the region is as follows
 . Then, using the previous results, we get that
. Then, using the previous results, we get that
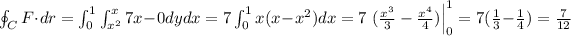 (circulation)
(circulation)
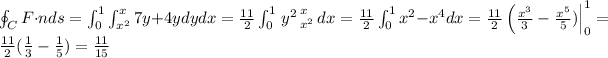 (flux)
(flux)