Question

The number of bacteria in a Petri dish was initially determined to be 1. After one hour, the number of bacteria had increased to 3 and after another hour to 6. Assume that the rate of growth of bacteria in the dish at any time t can be calculated using the logistic equation

dB/dt =B(a-bB)

(a) Determine the number of bacteria in the dish after an additional hour has passed.

(b) Determine the carrying capacity of the dish based on the developed logistic equation.

Answer 1

a) the number of bacteria in the dish after an additional hour has passed = 8

b) the carrying capacity of the dish based on the developed logistic equation. = 9

Explanation:

Given that ;

The Logistic growth model is :

`(dB)/(dt)= B (a-bB)`

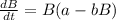
Solving the above equation ; we have a MODEL EQUATION;

`B_t = (aB_o)/(bB_o+(a-bB_o)e^(-at))`

in which:

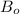`B_o` represents the initial population of the bateria.

We are given that the number of the bacteria in the Petri dish was initially determined to be 1 , then ;

`B_t = (a*1)/(b*1+(a-b*1)e^(-at))`

`B_t = (a)/(b+(a-b)e^(-at))`

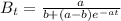
After an hour ; we were told that the number of the bacteria increased to 3 ; So:

`3 = (a)/(b+(a-b)e^(-a(1)))`

`3b+3(a-b)e^(-a) =a ---- equation (1)`

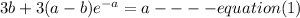
Similarly after (2) hours; the number of the bacteria increased to 6; then

`6 = (a)/(b+(a-b)e^(-a(2)))`

`6b+6(a-b)e^(-2a) =a ---- equation (2)`

So;

`3b+3(a-b)e^(-a) =a ---- equation (1)`

`6b+6(a-b)e^(-2a) =a ---- equation (2)`

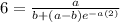
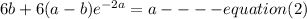
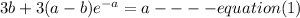
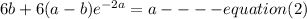
Solving for a and b from the above two eqautions: Then,

a = 1.386

b = 0.154

Substituting the value of a and b into our MODEL EQUATION; we have

`B_t = (1.386)/(0.154+(1.386-0.154*1)e^(-1.386t))`

`B_t = (1.386)/(0.154+1.232e^(-1.386t))`

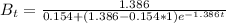
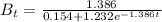
a) Determine the number of bacteria in the dish after an additional hour has passed.

i.e at t = 3

`B = (1.386)/(0.154+1.232e^(-1.386(3)))`

`B = (1.386)/(0.154+1.232 * 0.01563)`

`B= (1.386)/(0.173267)`

`B = 7.9992`

`B= 8`

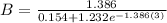
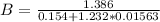
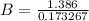
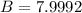
b) Determine the carrying capacity of the dish based on the developed logistic equation.

The carrying capacity B can be expressed as :

`B = (a)/(b)`

`B = (1.386)/(0.154)`

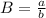
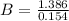
B =9