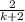What is the product? StartFraction 4 k + 2 Over k squared minus 4 EndFraction times StartFraction k minus 2 Over 2 k + 1 EndFraction

Question

asked Aug 25, 2021 92.9k views

2 Answers

Msfanboy · Answer 1 · 2021-08-27T10:10:38+0000

Answer:

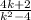(4k + 2)/(k^(2)-4 ) ×
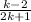(k-2)/(2k+1) =
(2)/(k + 2)

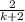
Explanation:

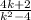(4k + 2)/(k^(2)-4 ) ×
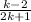
(k-2)/(2k+1)

To solve the above, we need to follow the steps below;

4k+2 can be factorize, so that;

4k +2 = 2 (2k + 1)

k² - 4 can also be be expanded, so that;

k² - 4 = (k-2)(k+2)

Lets replace 4k +2 by 2 (2k + 1)

and

k² - 4 by (k-2)(k+2) in the expression given

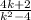(4k + 2)/(k^(2)-4 ) ×
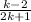
(k-2)/(2k+1)

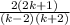(2(2k+ 1))/((k-2)(k+2)) ×
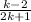
(k-2)/(2k+1)

(2k+1) at the numerator will cancel-out (2k+1) at the denominator, also (k-2) at the numerator will cancel-out (k-2) at the denominator,

So our expression becomes;

(2)/(k + 2)

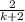
Therefore,
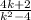(4k + 2)/(k^(2)-4 ) ×
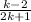(k-2)/(2k+1) =
(2)/(k + 2)