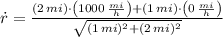Question

A plane flying horizontally at an altitude of 1 mi and a speed of 1000 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 2 mi away from the station.

A. 500√ 3 mi/h
B. 370 mi/h
C. 175/ √ 5 mi/h
D. 250√ 5 mi/h

Answer 1

`\dot r = 894.427\,(mi)/(h)`
`\left(500√(3)\,(mi)/(h) \right)`

Explanation:

The trigonometrical equation of the distance between the radar station and the plane is given by the Pythagorean Theorem:

`r^(2) = x^(2) + y^(2)`

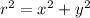
Where:

`x` - Horizontal distance of the plane with respect to the radar station, in miles.

`y` - Vertical distance of the plane with respect to the radar station, in miles.

The rate at which the distance from the plane to the station is increasing is found by deriving the previous expression regarding time and replacing all known expressions:

`2\cdot r \cdot \dot r = 2\cdot x \cdot \dot x + 2\cdot y \cdot \dot y`

`\dot r = \frac{x\cdot \dot x + y \cdot \dot y}{\sqrt{x^(2)+y^(2)}}`

`\dot r = \frac{(2\,mi)\cdot \left(1000\,(mi)/(h) \right)+(1\,mi)\cdot \left(0\,(mi)/(h) \right)}{\sqrt{(1\,mi)^(2)+(2\,mi)^(2)}}`

`\dot r = 894.427\,(mi)/(h)`