Answer:
The rate of change of the surface area is 2,629 inches per minute.
Explanation:
Given that,
The height is decreasing at a rate of 11.5 inches per minute and the radius of a right circular cylinder is increasing at a rate of 9.5 inches per minute.
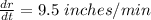
and
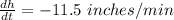
r = radius of the right circular cylinder
h= height of the right circular cylinder
The surface area of the right circular cylinder= 2π(r²+rh)
A=2π(r²+rh)
Differentiating with respect to t
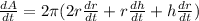
Now plug the value of
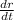 and
and
 .
.
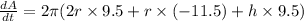
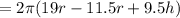
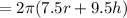
The rate of change of the surface area when the height is 31 inches and radius is 16.5 inches.
r = 16.5 inches, h = 31 inches
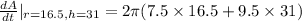
=2,629 inches per minute
The rate of change of the surface area is 2,629 inches per minute.