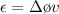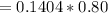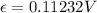Question

An MRI scanner is based on a solenoid magnet that produces a large magnetic field. The magnetic field doesn't stop at the solenoid's edge, however, but extends into the area around the magnet. Suppose a technician walks toward the scanner at 0.80 m/s from a region 1.0 m from the scanner where the magnetic field is negligible, into a region next to the scanner where the field is 6.0 T and points horizontally. As a result of this motion, what is the maximum magnitude of the change in flux through a loop defined by the outside of the technician's head? Assume the loop is vertical and has a circular cross section with a diameter of 19 cm.

What is the magnitude of the average induced emf around the outside of the technician's head during the time she's moving toward the scanner?

Answer 1

The maximum change in flux is
`\Delta \o = 0.1404 \ Wb`

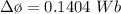
The average induced emf
`\epsilon =0.11232 V`

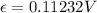
Step-by-step explanation:

From the question we are told that

The speed of the technician is
`v = 0.80 m/s`

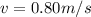
The distance from the scanner is
`d = 1.0m`

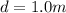
The initial magnetic field is
`B_i = 0T`

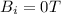
The final magnetic field is
`B_f = 6.0T`

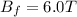
The diameter of the loop is
`D = 19cm = (19)/(100) = 0.19 m`

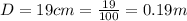
The area of the loop is mathematically represented as

`A = \pi [(D)/(2) ]^2`

`= 3.142 (0.19)/(2)`

`= 0.02834 m^2`

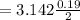
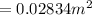
At maximum the change in magnetic field is mathematically represented as

`\Delta \o = (B_f - B_i)A`

=>
`\Delta \o = (6 -0)(0.02834)`

`\Delta \o = 0.1404 \ Wb`

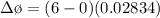
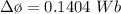
The average induced emf is mathematically represented as

`\epsilon = \Delta \o v`

`= 0.1404 * 0.80`

`\epsilon =0.11232 V`