Question

The slopes of perpendicular lines are ___ ___of each other, which means their products is -1.

A. fractional reciprocals
B. negative reciprocals
C. positive reciprocals ​

Answer 1

Negative Reciprocals

Explanation:

Consider two slopes being perpendicular to each other:

`\displaystyle \large{m_1\cdot m_2=-1}`

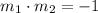
You will either receive:

`\displaystyle \large{m_1=-(1)/(m_2)}`

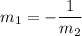
or:

`\displaystyle \large{m_2=-(1)/(m_1)}`

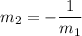
Say, you want to find perpendicular slope of 4. You have first slope as 4 and another as unknown which is assigned as m variable:

`\displaystyle \large{4m=-1}\\\displaystyle \large{m=-(1)/(4)}`

Therefore, 4 and -1/4 are perpendicular to each other. See that one slope is positives while another is negative. If you have negative slope then the perpendicular slope is positive.

Hence, they are indeed reciprocal but also negative as well.