Question

Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 144 millimeters, and a variance of 49. If a random sample of 50 steel bolts is selected, what is the probability that the sample mean would differ from the population mean by more than 2.6 millimeters

Answer 1

0.0086

Explanation:

Answer 2

The probability that the sample mean would differ from the population mean by more than 2.6 mm is 0.0043.

Explanation:

According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and appropriately huge random samples (n > 30) are selected from the population with replacement, then the distribution of the sample means will be approximately normally distributed.

Then, the mean of the distribution of sample mean is given by,

`\mu_(\bar x)=\mu`

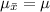
And the standard deviation of the distribution of sample mean is given by,

`\sigma_(\bar x)=(\sigma)/(√(n))`

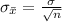
The information provided is:

μ = 144 mm

σ = 7 mm

n = 50.

Since n = 50 > 30, the Central limit theorem can be applied to approximate the sampling distribution of sample mean.

`\bar X\sim N(\mu_(\bar x)=144, \sigma_(\bar x)^(2)=0.98)`

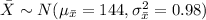
Compute the probability that the sample mean would differ from the population mean by more than 2.6 mm as follows:

`P(\bar X-\mu_(\bar x)>2.6)=P((\bar X-\mu_(\bar x))/(\sigma_(\bar x)) >(2.6)/(√(0.98)))`

`=P(Z>2.63)\\=1-P(Z<2.63)\\=1-0.99573\\=0.00427\\\approx 0.0043`

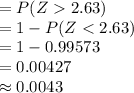
*Use a z-table for the probability.

Thus, the probability that the sample mean would differ from the population mean by more than 2.6 mm is 0.0043.