Question

Rewrite x^2 + 6x +15 in the form of a perfect square and a constant

Answer 1

`(x+3)^(2)+6`

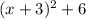
Explanation:

The given expression is:

`x^2+6x+15`

We have to re-write the given expression in form of perfect square. The above equation can be rewritten as:

`(x^2+6x)+15\\\\ =(x^2+2(x)(3))+15`

The general formula of a perfect square is:

`(a+b)^(2)=a^(2)+2(a)(b)+b^(2)`

Comparing previous two equations we can conclude that:

We have the square of first term(x), we have twice the product of first term(x) and second term(3). The square of second term(3) is missing. We can rewrite the previous equation as:

`(x^2+2(x)(3))+9+6\\\\ =(x^2+2(x)(3)+9)+6\\\\ =(x^2+2(x)(3)+3^(2))+6\\\\ =(x+3)^(2)+6`

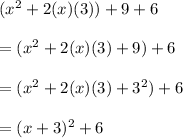
This is the required form of the given expression.