Question

Choose all that correctly define the point on the directed line segment between the two given points that partitions the segment in the given ratio

Line segment AB has endpoints A(5, 4) and B(2,7). The coordinates (4,5) divides the line segment directed

from A to B in the ratio of 1:2


Line segment AB has endpoints A(6,5) and B(3,8). The coordinates (5,6) divides the line segment directed

from A to B in the ratio of 1:2.


Line segment AB has endpoints A(5,7) and B(8,4). The coordinates (6,5) divides the line segment directed

from A to B in the ratio of 1:2.


Line segment AB has endpoints A(7, 2) and B(4,8). The coordinates (5, 4) divides the line segment directed

from A to B in the ratio of 1:2.

Answer 1

A and B

Explanation:

If point P (x,y) lies on line segment
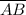`\overline{AB}` (between points A and B) and satisfies AP:PB=m:n, then we say that P divides
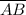`\overline{AB}` internally in the ratio m:n. The point of division has the coordinates

`P=\left( (mx_2 + nx_1)/(m+n), (my_2 + ny_1)/(m+n) \right).`

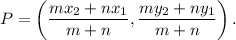
CORRECT

• Line segment AB has endpoints A(5, 4) and B(2,7). The coordinates (4,5) divides the line segment directed from A to B in the ratio of 1:2

`P=\left( (1*2 + 2*5)/(2+1), (1*7 + 2*4)/(2+1) \right)=(4,5)`

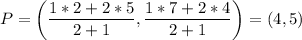
• Line segment AB has endpoints A(6,5) and B(3,8). The coordinates (5,6) divides the line segment directed from A to B in the ratio of 1:2.

`P=\left( (1*3 + 2*6)/(2+1), (1*8 + 2*5)/(2+1) \right)=(5,6)`

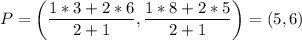
INCORRECT

• Line segment AB has endpoints A(5,7) and B(8,4). The coordinates (6,5) divides the line segment directed from A to B in the ratio of 1:2.

`P=\left( (1*8 + 2*5)/(2+1), (1*4 + 2*7)/(2+1) \right)=(5,6)`

• Line segment AB has endpoints A(7, 2) and B(4,8). The coordinates (5, 4) divides the line segment directed from A to B in the ratio of 1:2.

`P=\left( (1*4 + 2*7)/(2+1), (1*8 + 2*2)/(2+1) \right)=(6,4)`

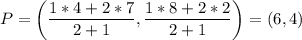
REMARK

A and B are correct. However the coordinates of P for C and D are incorrect.