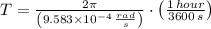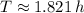Answer:
a)
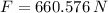 , b)
, b)
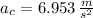 , c)
, c)
 ,
,
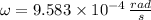 , d)
, d)
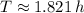
Step-by-step explanation:
a) The gravitational force exerted by the Earth on the satellite is:

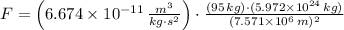
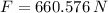
b) The centripetal acceleration of the satellite is:
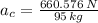
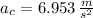
c) The speed of the satellite is:
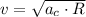
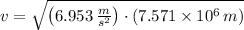

Likewise, the angular speed is:
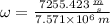
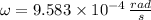
d) The period of the satellite's rotation around the Earth is: