Solution
S = 15 x
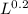 x
x
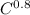
Total cost, T = wL + rC = 50L + 100C
Total revenue, R = Output price (P) x Quantity = P x 15 x
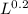 x
x
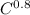
(a)
Optimization problem will be:
Max R = P x 15 x
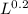 x
x
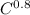
Subject to T = 50L + 100C
(b) When S = 50,000
Cost is minimized when (MPL / MPC) = w / r
MPL =
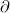 R /
R /
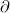 L = P x 15 x 0.2 x
L = P x 15 x 0.2 x
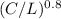 = P x 3 x
= P x 3 x
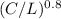
MPC =
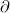 R /
R /
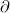 C = P x 15 x 0.8 x
C = P x 15 x 0.8 x
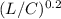 = P x 12 x
= P x 12 x
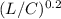
MPL / MPC = (3/12) x (C / L) = 50/100
C / 4L = 1/2
4L = 2C
2L = C
Substituting in production function,
15 x
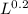 x
x
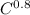 = S
= S
15 x
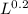 x
x
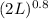 = 50,000
= 50,000
15 x
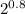 x
x
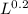 x
x
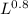 = 50,000
= 50,000
L = 50,000 / (15 x 20.8)
L = 1,914.50
C = 2L = 3,829.00
Total cost ($) = 50 x 1,914.50 + 100 x 3,829.00 = 95,725.00 + 382,900 = 478,625.00
Note: This optimization problem can be solved without using Solver too, as shown here.