Question

A box is created from a square piece of cardboard 6 in. on a side by cutting a square from each corner and folding up the sides. Let x represent the length of the sides of the squares removed from each corner. box Write a function representing the volume of the box, V(x). Write as a polynomial in standard form. Note: To write a polynomial in standard form, remember, you must multiply everything out.

Answer 1

The function which represents the volume of the box

V(x)=4x³-24x²+36x

where V(x) is in cubic inches.

Explanation:

Cuboid:

• Cuboid is a three dimension shape.
• It has 6 faces and 8 vertices.
• The length of diagonals is
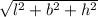  `√(l^2+b^2+h^2)` . l= length, b= width and h= height.
• The total surface area is = 2(lb+bh+lh)
• Volume is = length ×width× height

Given that,

The dimensions of the cardboard is 6 inches by 6 inches.

The length of the side of the squares that removed from each corners of the cardboard is represented by x.

Then, the length of the box is = (6-2x) inches.

The width of the box is = (6-2x) inches

The height of the box is = x inches.

The volume of the box is= length ×width× height

=(6-2x)(6-2x) x cubic inches

={6(6-2x)-2x(6-2x)}x cubic inches

={36-12x-12x+4x²}x cubic inches

={36-24x+4x²}x cubic inches

=(36x-24x²+4x³) cubic inches

=(4x³-24x²+36x) cubic inches

The function which represents the volume of the box

V(x)=4x³-24x²+36x

where V(x) is in cubic inches.