Question

An elementary school is offering 3 language classes: one in Spanish, one in French, and one in German. These classes are open to any of the 86 students in the school. There are 38 in the Spanish class, 27 in the French class, and 16 in the German class. There are 14 students that in both Spanish and French, 6 are in both Spanish and German, and 5 are in both French and German. In addition, there are 2 students taking all 3 classes. If one student is chosen randomly, what is the probability that he or she is taking at least one language class

Answer 1

Answer: The required probability is 0.674.

Explanation:

Since we have given that

Number of students in the Spanish class = 38

Number of students in the French class = 27

Number of students in the German class = 16

Number of students in both spanish and French = 14

Number of students in both Spanish and German = 6

Number of students in both French and German = 5

Number of students in all three class = 2

So, it becomes:

`n(S\cup F\cup G)=n(S)+n(F)+n(G)-n(S\cap F)-n(G\cap F)-n(S\cap G)+n(S\cap F\cap G)\\\\n(S\cup F\cup G)=38+27+16-14-5-6+2=58`

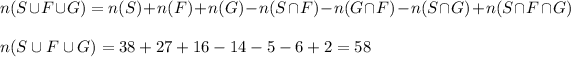
So, Probability that he or she is taking at least one language class is given by

`(58)/(86)=0.674`

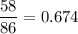
Hence, the required probability is 0.674.