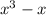Question

Find the L.C.M of x^2+x , x^2-1 , x^2-x

Answer 1

`x\cdot(x+1)\cdot(x-1)=x^3-x`

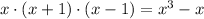
Explanation:

To find the LCM of any integer, we take the product of all the highest powers of the factors that appear in the numbers. Factoring our three given expressions gives us the products

`x^2+x=x\cdot(x+1)\\x^2-1=(x+1)\cdot(x-1)\\x^2-x=x\cdot(x-1)\\`

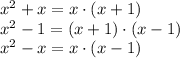
Our LCM will be a product of some powers of
`x`,
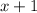`x+1`, and
`x-1`. The most each factor occurs in the three expressions is once, so our least common multiple is

`x^1\cdot(x+1)^1\cdot(x-1)^1`

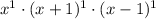
which can be simplified to
`x^3-x`

Answer 2

Explanation:

x² + x = x * (x + 1)

x² - 1 = (x - 1)(x + 1) {a² - b² = (a+b)(a-b)}

x² - x = x * (x - 1)

LCM = x * (x + 1) * (x - 1)