Question

4 ^(1+2x)=1024 how do I express each side as a power of the same base and then equate exponents?

Answer 1

I'll help a bit!

So, we need to have the same base on either side, like this:

`EX:4^(7) =4^(x)`

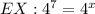
Essentially, we need to find the factors of 1024:

`1024=4*4*4*4*4`

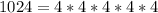
So then, we can write it as:

`4^(1+2x) =4^(5)`

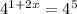
(As there are 5 4's in the factorization)

So, let's solve!

First step, use the Equality of Bases Property:

It states that:

`x^(v) =x^(c)`

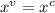
Then:

`v=c`

So, continuing on:

`1+2x=5\\2x=4\\x=2`

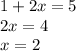
Hope this helps!

(hope this also answers your question)

P.S. Ask me if you have any more questions, and remember to wash your hands!