Question

The spread of a virus through a city is modeled by the function N=25,000/1+100e^-0.5t, where N is the number of people infected by the virus after t days. How many days does it take for 1,500 people in this city to be infected with the virus?

Answer 1

t = 3.7 days

Explanation:

The spread of a virus through a city is modeled by the function N=25,000 / (1+100 e ^-0.5t),

1500 = 25000 / (1 + 100 e ^-0.5t)

1500 / (1 + 100 e ^-0.5 t) = 25000

1 + 100 e ^ - 0.5 t = 25000 / 1500

1 + 100 e ^ -0.5 t = 16.667

100 e ^-0.5 t = 16.667 - 1

100 e ^0.5 t = 15.667

e ^-0.5 t = 15.667 / 100

e ^-0.5 T = 0.1567

ln e ^0-0.5 t = ln 0.1567

- 0.5 t = - 1.8534

t = -1.8534 / - 0.5

t = 3.7 days

Answer 2

We have been given that the of a virus through a city is modeled by the function
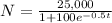`N=(25,000)/(1+100e^(-0.5t))`, where N is the number of people infected by the virus after t days. We are asked to find the number of days it will take for 1,500 people in this city to be infected with the virus.

To solve our given problem, we will substitute
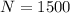`N=1500` in our given equation and solve for t.

`1500=(25,000)/(1+100e^(-0.5t))`

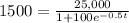
Multiply both sides by
`(1+100e^(-0.5t))`.

`1500\cdot (1+100e^(-0.5t))=(25,000)/(1+100e^(-0.5t))\cdot (1+100e^(-0.5t))`

`1500\cdot (1+100e^(-0.5t))=25,000`

`(1500\cdot (1+100e^(-0.5t)))/(1500)=(25,000)/(1500)`

`1+100e^(-0.5t)=(50)/(3)`

`1-1+100e^(-0.5t)=(50)/(3)-1`

`100e^(-0.5t)=(50)/(3)-(3)/(3)`

`100e^(-0.5t)=(47)/(3)`

`(100e^(-0.5t))/(100)=((47)/(3))/(100)`

`e^(-0.5t)=(47)/(300)`

`\text{ln}(e^(-0.5t))=\text{ln}((47)/(300))`

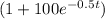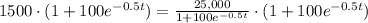
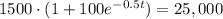
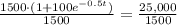
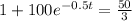
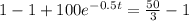
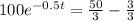
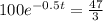
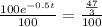
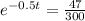
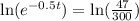
Using natural log property
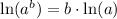`\text{ln}(a^b)=b\cdot \text{ln}(a)`, we will get:

`-0.5t\cdot \text{ln}(e)=\text{ln}((47)/(300))`

`-0.5t\cdot 1=\text{ln}((47)/(300))`

`-0.5t=-1.853634872946`

`(-0.5t)/(-0.5)=(-1.853634872946)/(-0.5)`

`t=3.707269\approx 3.71`

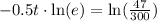
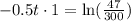
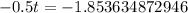
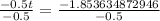
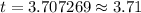
Therefore, it will take approximately 3.71 days for 1,500 people in this city to be infected with the virus.