Question

Find the angle between the given vectors to the nearest degree.

a.
110.7
c.
108.4
b.
71.6
d.
112.5

Answer 1

Given:

Given that the two vectors are u = (7,-4) and v = (1,5)

We need to determine the angle between these two vectors.

Dot product of u and v:

The dot product of u and v is given by

`u \cdot v=(7 * 1)+(-4 * 5)`

`=7-20`

`u \cdot v=-13`

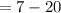
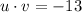
Magnitude of u:

The magnitude of u is given by

`\| u \|=√((7)^2+(-4)^2)`

`\| u \|=√(49+16)`

`\| u \|=√(65)`

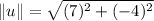
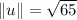
Magnitude of v:

The magnitude of v is given by

`\| v \|=√((1)^2+(5)^2)`

`\| v \|=√(1+25)`

`\| v \|=√(26)`

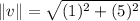
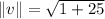
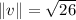
Angle between the two vectors:

The angle between the two vectors can be determined using the formula,

`cos \ \theta=(u \cdot v)/(\| u \| \| v \|)`

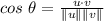
Substituting the values, we get;

`cos \ \theta=(-13)/(√(65) √(26) )`

`cos \ \theta=(-13)/(41.11 )`

`cos \ \theta=-0.316`

`\theta=cos ^(-1)(-0.316)`

`\theta=108.4^(\circ)`

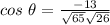
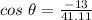
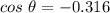
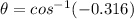
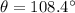
Thus, the angle between the two vectors is 108.4°