Question

In ΔVWX, x = 10 cm, ∠X=126° and ∠V=13°. Find the length of w, to the nearest 10th of a centimeter.

Answer 1

8.1

Explanation:

delta math told me so

Answer 2

Length of side
`VW= 36.81\ cm`.

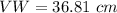Explanation:

Diagram of the given scenario is shown below.

Given that:
`\angle X=126`° ,
`\angle V=13`° and
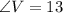`XW =10\ cm`

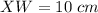
To find : Length of
`VW` ?

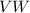So, In
`\triangle VWX`

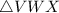
Using Sine law :- Sine law states that the ratio of each side of triangle the sine of the opposite angle is the equal for all three sides and angles. let sides and angle are
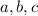`a,b,c` and
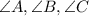`\angle A,\angle B,\angle C` then

Sine law :
`(a)/(Sin\angle A) =(b)/(Sin\angle B) =(C)/(Sin\angle C)`

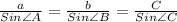
According to Question,

Applying Sine law in
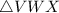`\triangle VWX` we get,

`(VW)/(Sin\angle 126) =(10)/(Sin\angle13)`

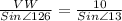
By cross-multiplication

`VW =(10 * Sin\angle 126)/(Sin\angle13) = (10*0.81)/(0.22) =36.81`

Therefore, Length of side
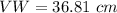`VW= 36.81\ cm`.