Question

In traveling across flat land, you notice a mountain directly in front of you. Its angle of elevation (to the peak) is . After you drive x = 23 km closer to the mountain, the angle of elevation is . Find the height of the mountain (round to one decimal place). Just enter the height value with one decimal. Do not enter the unit.

Answer 1

In traveling across flat land, you notice a mountain directly in front of you. Its angle of elevation (to the peak) is 3.5°. After you drive x = 13 km closer to the mountain, the angle of elevation is 9°. Find the height of the mountain (round to one decimal place). Just enter the height value with one decimal. Do not enter the unit.

The height of the mountain is 1.2 km without unit it is only 1.2

Explanation:

Given:

Two angle of elevation.

We have to find the height of the mountain.

Let the height be "h" .

Note:

Angle of elevation will increase as we move closer to the object.

Considering the distance from 3.5 ° as (13+x) km

Using trigonometric ratios:

For adjacent side "x".

⇒
`tan(\theta) = (opposite)/(adjacent)`

⇒
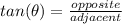
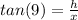`tan(9) = (h)/(x)` ...equation (i)

⇒
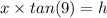`x* tan(9) = h` ...equation (ii)

For adjacent side "(13+x)"

⇒
`tan(\theta) = (opposite)/(adjacent)`

⇒
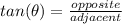
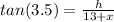`tan(3.5) = (h)/(13+x)` ...equation (iii)

Dividing equation (i) and (iii).

⇒
`(tan(9))/(tan(3.5)) =(h)/(x)* (13+x)/(h)`

⇒
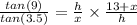
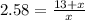`2.58 =(13+x)/(x)` ...cross multiplication

⇒
`2.58x=13+x`

⇒
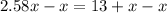`2.58x-x=13+x-x` ...subtract x both side

⇒
`1.58x=13`

⇒
`x=(13)/(1.58)`

⇒
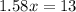
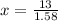
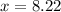`x=8.22` km

Plugging x=8.22 km in equation (ii) we can find h that is the height of the mountain.

So,

⇒
`x* tan(9) = h`

⇒
`8.22* 0.15 =h`

⇒
`1.23 = h`

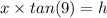
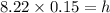
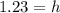
The height of the mountain is 1.23 km with one decimal it is 1.2 km only.