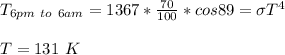Question

Imagine that the Earth had no atmosphere and was covered with a material that was a perfect thermal insulator (and zero thermal inertia) that reflected 30 % of impinging sunlight back into space. The temperature of any point on the surface was determined by the power density of adsorbed sunlight being exactly matched by the power density radiated back into space (sT4 ), where s is the Stefan Boltzmann constant (5.67 x 10-8 W m-2 K-4 ) and T is the temperature in Kelvin. For a location on the equator, what would be the ground temperature (degrees K) at these four times; A) noon (sun overhead), B) at 3 pm (Sun 45 degrees from overhead), C) sunset and D) midnight.

Answer 1

`T_(12 \ pm) = 360 \ K`

`T_(3 \ pm) = 330 \ K`

`T = 131\ K`

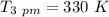
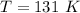
Step-by-step explanation:

The power of sunlight at equator
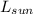`L_(sun)` is known to be =
`3.846*10^(26) \ W`

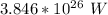
Distance = 1 Au =
`1.496*10^(11) \ m`

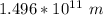
Thus; the power at equator =
`(3.846*10^(26))/(4 \pi *(1.496*10^(11))^2)`

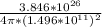
= 1367 W/m²

Now; at noon (sun overhead)

`1367* (70)/(100)= 5.67*20^(-8)*T^4\\\\T^4 =(956.9)/(5.67*10^(-8))\\\\T^4 = 1.687*10^(10)\\\\T_(12 \ pm) = 360 \ K`

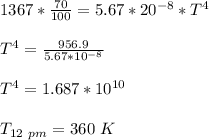
At 3 pm (Sun 45 degrees from overhead);

`1367* (70)/(100)*cos \ 45 = 5.67*20^(-8)*T^4\\\\T^4 =(676.63)/(5.67*10^(-8))\\\\T^4 = 1.193*10^(10)\\\\T_(3 \ pm) = 330 \ K`

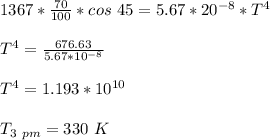
C) sunset and D) midnight.

We based our assumption on the notion that the incident angle at sunset and midnight be just below 90° ; for example . let say:

`T_(6pm \ to \ 6 am) = 1367* (70)/(100)*cos 89 = \sigma T^4\\ \\T = 131\ K`