Question

Of the cars sold during the month of July, 89 had air conditioning, 99 had an automatic transmission, and 74 had power steering. 5 cars had all three of these extras. 24 cars had none of these extras. 24 cars had only air conditioning, 65 cars had only automatic transmissions, and 26 cars had only power steering. 11 cars had both automatic transmission and power steering.

How many cars had air conditioning and automatic transmission but not power steering?

Answer 1

There are a total of 23 cars with air conditioning and automatic transmission but not power steering

Explanation:

Let A be the cars that have Air conditioning, B the cars that have Automatic transmission and C the cars that have pwoer Steering. Lets denote |D| the cardinality of a set D.

Remember that for 2 sets E and F, we have that

`|E \cup F| = |E| + |F| - |E \cap F|`

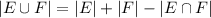
Also,

|E| = |E ∩F| + |E∩F^c|

We now alredy the following:

|A| = 89

|B| = 99

|C| = 74

`|A \cap B \cap C| = 5`

|(A \cup B \cup C)^c| = 24

|A \ (B U C)| = 24 (This is A minus B and C, in other words, cars that only have Air conditioning).

|B \ (AUC)| = 65

|C \ (AUB)| = 26

`|B \cap C| = 11`

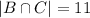
We want to know |(A∩B) \ C|. Lets calculate it by taking the information given and deducting more things

For example:

99 = |B| = |B ∩ C| + |B∩C^c| = 11 + |B∩C^c|

Therefore, |B∩C^c| = 99-11 = 88

And |A ∩ B ∩ C^c| = |B∩C^c| - |B∩C^c∩A^c| = |B∩C^c| - |B \ (AUC)| = 88-65 = 23.

This means that the amount of cars that have both transmission and air conditioning but now power steering is 23.