Question

A produce distributor uses 786 packing crates a month, which it purchases at a cost of $9 each. The manager has assigned an annual carrying cost of 35 percent of the purchase price per crate. Ordering costs are $27. Currently the manager orders once a month.

How much could the firm save annually in ordering and carrying costs by using the EOQ?

Answer 1

The firm save $385.308 annually in ordering and carrying costs by using the EOQ

Step-by-step explanation:

Given:

• Demand in a month (u) : 786 => the demand in a year (D): 786*12 = 9432
• The holding cost :35 percent of the purchase price per crate (C) = 0.35*9 =$3.15
• Ordering costs (O) : $27

To find the money the company can save when ordering based on the EOQ, we use the following formula to find the EOQ:

EOQ =
`\sqrt{ (2* D* O)/(C)}` =
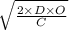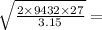`\sqrt{ (2* 9432* 27)/(3.15)}=` $402.1

• The total cost using the EOQ

= [(EOQ / 2) x C] + [(D / EOQ) x 0]

= (402.1 /2)*3.15 + (9432 / 402.1) x 27

= $1266.642

• The actual total annual inventory cost:

TC = [(u / 2) x C] + [(D / u) x O]

= [(786 / 2) x 3.15] + [(9432 / 786) x 27]

= 1327.95 + 324

= $1651.95

• The difference between the actual total cost minus the EOQ cost is:

= $1651.95 - $1266.642

=$385.308

So the firm save $385.308 annually in ordering and carrying costs by using the EOQ