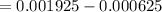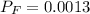Complete Question
The complete question is shown on the first uploaded image
Answer:
a
The probability is
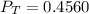
b
The probability is
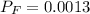
Explanation:
From the question we are told that
The mean for the exponential density function of bulbs failure is
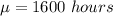
Generally the cumulative distribution for exponential distribution is mathematically represented as
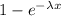
The objective is to obtain the p=probability of the bulbs failure within 1800 hours
So for the first bulb the probability will be
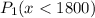
And for the second bulb the probability will be
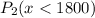
So from our probability that we are to determine the area to the left of 1800 on the distribution curve
Now the rate parameter
 is mathematically represented as
is mathematically represented as

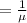
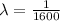
The probability of the first bulb failing with 1800 hours is mathematically evaluated as
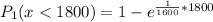
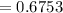
Now the probability of both bulbs failing would be

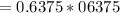
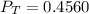
Let assume that one bulb failed at time
 and the second bulb failed at time
and the second bulb failed at time
 then
then
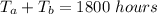
The mathematical expression to obtain the probability that the first bulb failed within between zero and
 and the second bulb failed between
and the second bulb failed between
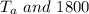 is represented as
is represented as
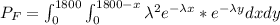

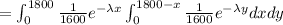
![=\int_(0)^(1800) {(1)/(1600) }e^(-\lambda x)[e^(- \lambda y)]\left {1800-x} \atop {0}} \right. dx](https://img.qammunity.org/2021/formulas/mathematics/high-school/tpz9412kwju0ah9eneu6m5vd4y2dy5p1qz.png)
![=\int_(0)^(1800) {(1)/(1600) }e^{-(x)/(1600) }[e^{- (1800 -x)/(1600) }-1] dx](https://img.qammunity.org/2021/formulas/mathematics/high-school/h0q976bnbexqrdnzicxl0izzkw3llea0r5.png)
![=[ {(1)/(1600) }e^{-(1800)/(1600) }-(1)/(1600)[e^{- (x)/(1600) }] \left {1800} \atop {0}} \right.](https://img.qammunity.org/2021/formulas/mathematics/high-school/4kxdegolmn36wswntk5hwr0pn9m7go6ody.png)
![=[ {(1)/(1600) }e^{-(1800)/(1600) }-(1)/(1600)[e^{- (1800)/(1600) }] -[[ {(1)/(1600) }e^{-(1800)/(1600) }-(1)/(1600)[e^(-0)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ot1mbg38vzl3y011z3puyftrcj53py0tj1.png)
![=[(1)/(1600) e^{-(1800)/(1600) } - (1)/(1600) e^(-0) ]](https://img.qammunity.org/2021/formulas/mathematics/high-school/h6267e4kvsggxbuyp6vcuxf553g1d51am0.png)